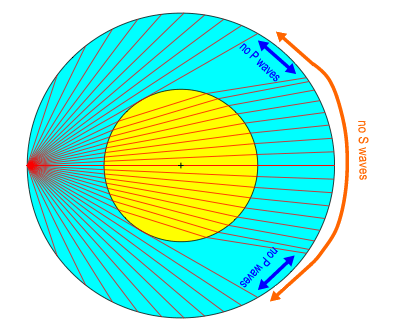
The core produces a "shadow zone" at the Earth's surface, into which seismic waves from A cannot travel.
Homework #3
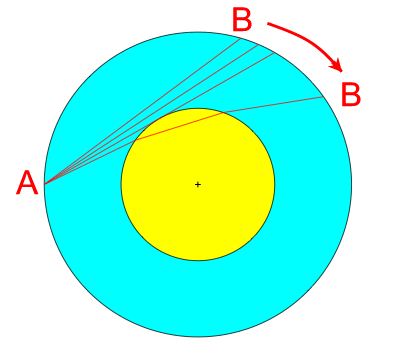
This diagram shows a schematic model of the Earth. We pretend that it just has two uniform layers, an outer high-velocity zone (light blue, representing the magnesium-silicate mantle) and a low-velocity core (yellow, representing liquid iron). Suppose that P waves travel from an earthquake source at A to a seismic detection station B which is moved to various points on the other side of the Earth as shown in the figure on the left. The figure on the right sketches wave paths from A to B for various positions of B, assuming that when the seismic waves reach the low-velocity core, the path is bent inward according to Fermat's principle.


The core produces a "shadow zone" at
the Earth's surface, into
which seismic waves from A
cannot travel.
Are S waves also excluded from the shadow zone? Explain why or why not.
The "shadow zone" at the
surface is actually a ring of points
opposite
to the earthquake source at A. Because of the focusing effect of the
low-velocity iron core, P waves are excluded from the shadow
zone. Now S waves can only travel in solid material, and they
can't travel in a liquid, as discussed in lecture. Therefore, the
shadow zone for S waves includes the shadow zone for P waves, but
covers the whole side of the
Earth opposite to A (see right-hand figure).
2. On average, the temperature beneath the Earth's crust
increases
at a rate of 20 degrees Centigrade per kilometer of depth. At
what
depth would water boil? (Assume the Earth's surface temperature
is
+20 degrees Centigrade and ignore the effect of increasing pressure on
the boiling point of water.) Show all calculations.
Water boils
at
100
C (at 1 bar pressure). Starting at an average temperature of +20
C, we need to go up 80 C more to reach the boiling point.
Dividing
80 C by the temperature gradient of 20 C/km, we get 4 km depth.
3. Using data for the values of the Earth's mass and mean
radius, verify that the average
density
of the Earth is 5515 kg/m3 (or 5.515 g/cm3).
Show all calculations.
Assume that
the
Earth
is a sphere of radius 6378 km = 6378 X 103 m.
Volume of the Earth
= 4 pi (6378 X 103 )3 / 3 = 1.087 X 1021
cubic meters.
Mass of the Earth
= 5.9736 X 1024 kg.
Average density
= 5.9736 X 1024 kg / 1.087 X 1021 cubic
meters
= 5497 kg/m3.
This approach gives
a number a little smaller than the value 5515 kg/m3 because
the Earth's actual volume is a little smaller due to oblateness.