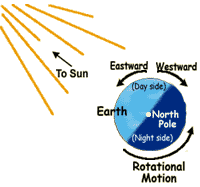
Why is it helpful to launch toward the east, from a place like Florida?
More
rocket
science!
A Hohmann transfer orbit trip to Mars would actually involve a series of rocket burns.
First, we need to get off the
surface of Earth and into a low "parking orbit".

Why is it helpful to launch toward the east, from a place like
Florida?

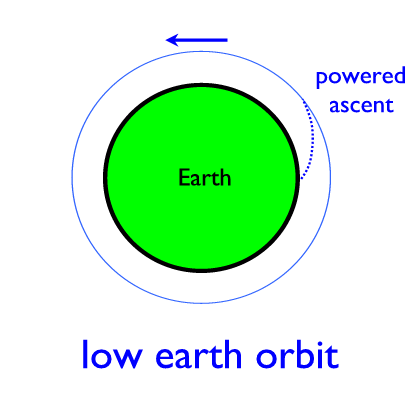
To achieve low Earth orbit, we need
an initial powered ascent to a velocity of about 7 km/s:
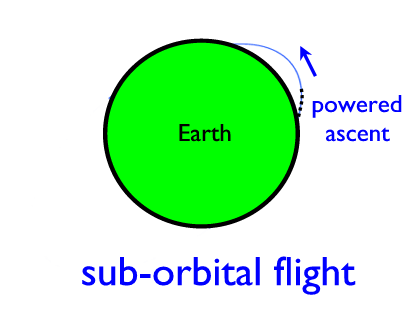
Suppose the rocket is launched with
a speed of, say, 1 km/s:
Now give it a bit more velocity (but still not enough to achieve
orbit):
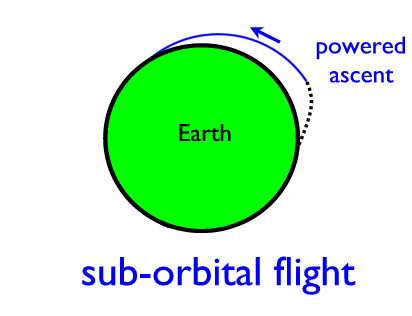
This is the principle of operation of ICBMs (Intercontinental
Ballistic Missiles).
Finally, if we launch to a final
speed of about 7 km/s, we get full Earth orbit.

Here is a link to a
YouTube movie that illustrates this point.
Next, we could apply a burn to go into a high-eccentricity ellipse (the Hohmann ellipse). The red arrow shows the direction of the necessary rocket thrust:
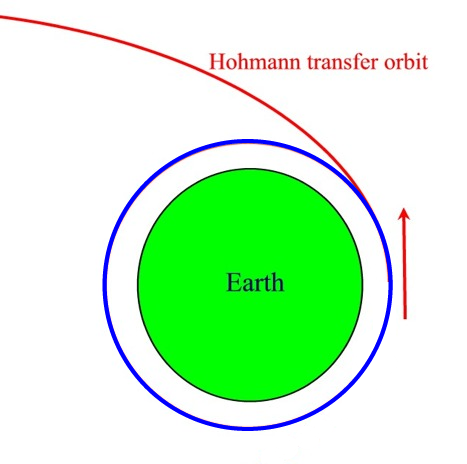
When we get to Mars, we need to "de-boost" from the Hohmann orbit into an orbit around Mars (the red arrow shows the direction of the de-boost rocket thrust):
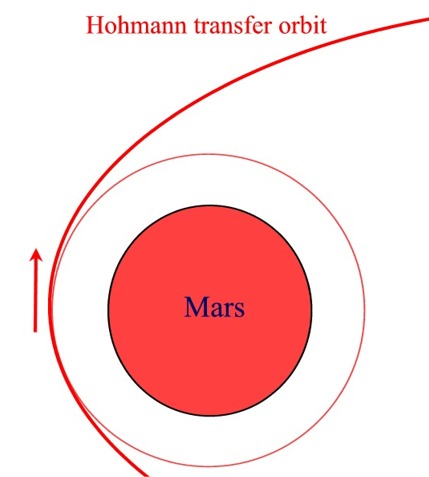
There are two different techniques
to de-boost:
(1) Fire the spacecraft's rocket
engines in the direction of motion of the spacecraft until we
have removed enough kinetic energy to go into orbit.
(2) If the planet has an atmosphere,
we can let atmospheric friction remove the spacecraft's extra
kinetic energy. This technique is called aerocapture:

Aerocapture can also be used to remove orbital energy from manned spacecraft, sometimes with tragic consequences:
Video of the
Columbia disaster
Figure 8 orbit
This strategy is used to go to the moon. We can make a close "fly-by" of the moon by launching the spacecraft into a special transfer orbit with a single boost out of Earth orbit, as shown in this figure:
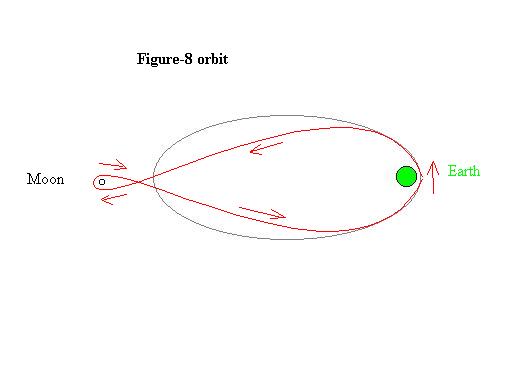
The gray ellipse shows the orbit we'd
get without the effect of lunar gravity. The red curve shows
(very schematically) what happens when the gravitational pull
of the Moon takes over at close distances from the Moon.
If we want to go into lunar orbit, we apply a reverse boost on
the farside of the Moon. To get back to the Earth, we do
everything in reverse. This strategy was used for the
successful lunar landing by Apollo 11.
The subsequent Apollo 13 mission (see movie starring Tom Hanks) had an onboard explosion and was forced to abort the plan to land on the moon. It didn't apply the farside deboost to get into lunar orbit. Instead, the spacecraft just kept going in its figure-8 orbit and automatically returned to Earth, where a deboost was applied to reenter the atmosphere.
The Lagrangian Points
Modern space exploration relies very heavily on using a careful balance of gravitational forces to minimize the number of rocket boosts ("burns"). The figure-8 orbital tour of the moon is based on mathematical work done two centuries ago by the great French mathematician and astronomer Joseph-Louis Lagrange, Count (comte) De L'empire. Here is a diagram showing the so-called Lagrangian points discovered by him:
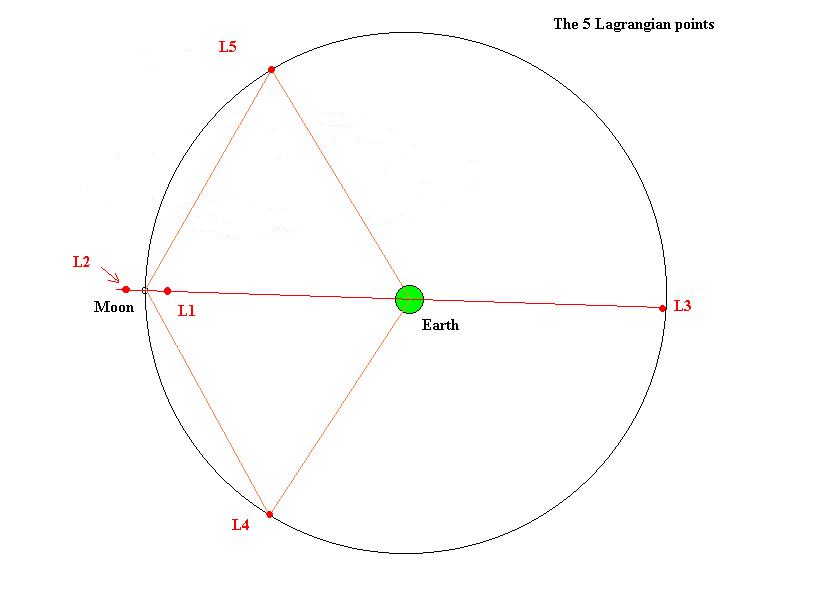
For a smaller body (the Moon) orbiting a larger body (the Earth), there are 5 points where rotational forces and gravitational forces acting on a spacecraft cancel out. The L1 point is where the Moon's gravity plus centrifugal force cancels the Earth's gravity. If we launch a spacecraft on a Hohmann transfer trajectory from the Earth to the Moon and aim it at L1, it will actually complete a figure-8 orbit of the type discussed above. Similarly, a spacecraft placed near any of the other 4 points will tend to hover there. The L4 and L5 points are on equilateral triangles at the same distance from the Earth as the Moon, but 60 degrees ahead and behind the Moon. They are more stable than the other 3 Lagrangian points, and some space advocates have suggested these as natural locations for human space colonies.
Obviously, the 5 Lagrangian points
also exist for the Earth with respect to the Sun, for Jupiter
with respect to the Sun, etc.
Using the Lagrangian points strategy, very complicated spacecraft missions have been devised. Here is one used by the ISEE3 satellite to visit the Earth's (not the Moon's) L1 and L2 points. The spacecraft used a final Moon encounter to visit two comets.
Here is a view of the Earth's
five Lagrange points, using a similar perspective:
It is important to understand that
all of these orbits discussed in today's lecture are not
Kepler orbits. That is because they involve three
bodies: the Earth, the Moon, and the spacecraft. And, the ISEE3
mission actually involves four bodies: the Earth,
the Moon, the Sun, and the spacecraft.
Kepler's theory only applies to two
bodies orbiting each other. When more than two bodies are
involved, the motion gets very complicated (as you can see from
the figure above), and simple figures like ellipses can't be
used to describe the motion. The only way to predict the
spacecraft's orbit is by using powerful computers.
Gravity assist
As you can see, ISEE3 left the Earth-Moon system by making use of a gravity assist from the Moon. How does this work?
As we have already mentioned, the force F between two bodies, one of mass m and the other of mass M, is given by
F = -GMm/ r2,
where r is the distance between the two bodies and G is a constant number called the Universal Gravitational Constant, or just gravitational constant. The minus sign is a convention that means the force is attractive -- it tries to pull the two bodies together.
In many cases in the solar system, one mass is very much bigger than the other (for example, the Sun is 300000 times the mass of the Earth). The two masses pull on each other with equal force, but the force has a much bigger effect on the motion of the small mass than on the motion of the big mass.
Suppose a big mass exerts an extra
force on a small mass. Imagine a tennis player hitting a
ball back to his opponent very hard:
The ball returns with more velocity than before it was hit!
But a tennis player could also play a "drop" shot by returning the ball with less velocity. He could do this by moving his racket backward as it meets the ball, thus taking velocity off the ball (a real drop shot uses lots of spin as well, but we'll ignore this).
The analog with spacecraft is
this: If a spacecraft meets a planet more or less
"head-on", the planet will add velocity to the spacecraft and
send it off in a new direction while exerting a gravitational
force on it. If a spacecraft meets a planet moving more or
less in the same direction, the encounter is like a drop shot --
it takes velocity off the spacecraft and drops it into a
lower-energy orbit.
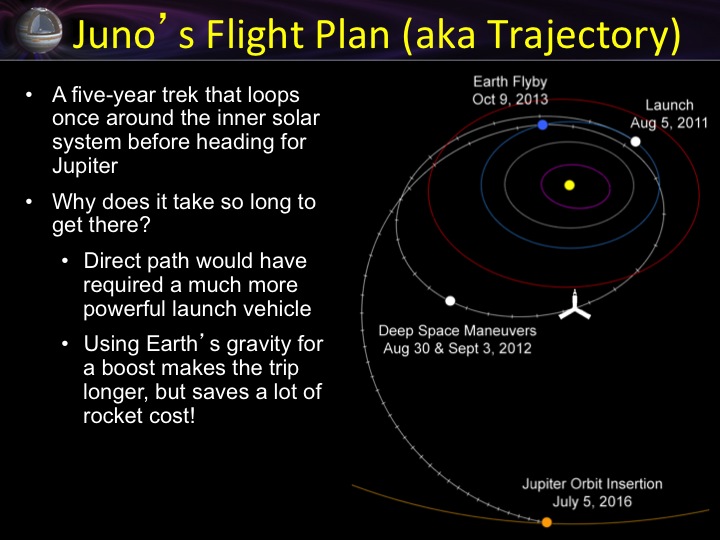
Here is the "flight plan" for my
current mission, Juno. Last fall, Juno was back at the
Earth, returning after more than 2 years in space. That
2-year loop around the Sun is analogous to a batter tossing a
ball up in order to hit it with his bat as it falls back
down. In October, the Earth hit a fungo to Jupiter!
Mission scientists can plan an
encounter of a spacecraft with planets to either add or subtract
kinetic energy from the spacecraft's orbit and thus change its
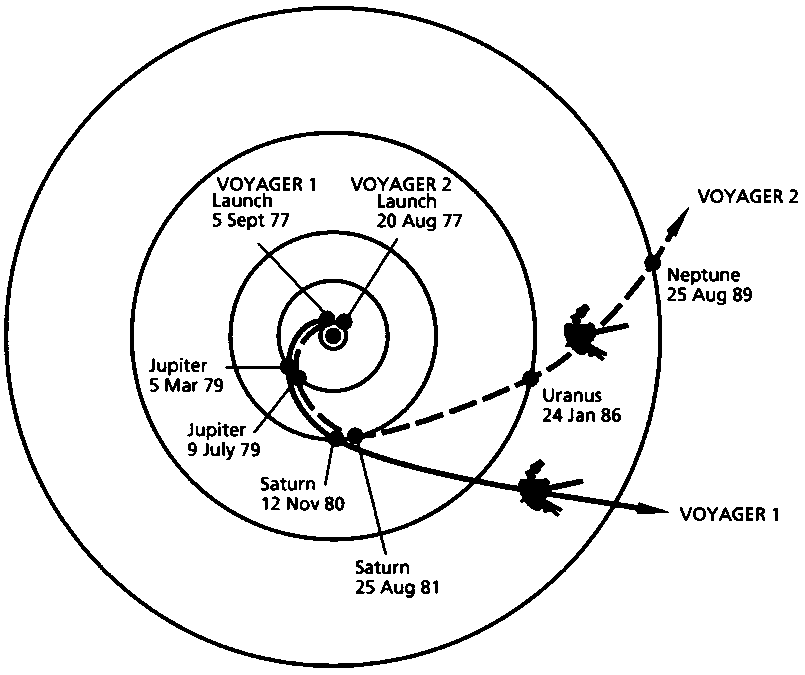
motion. One of the classic examples of this type of
orbital maneuver is the "Grand Tour" of the outer solar system
executed by the two Voyager spacecraft:
Escape velocity
When we launch a spacecraft from the surface of the Earth, the semimajor axis a of its orbital ellipse gets bigger and bigger as we increase the launch velocity v:
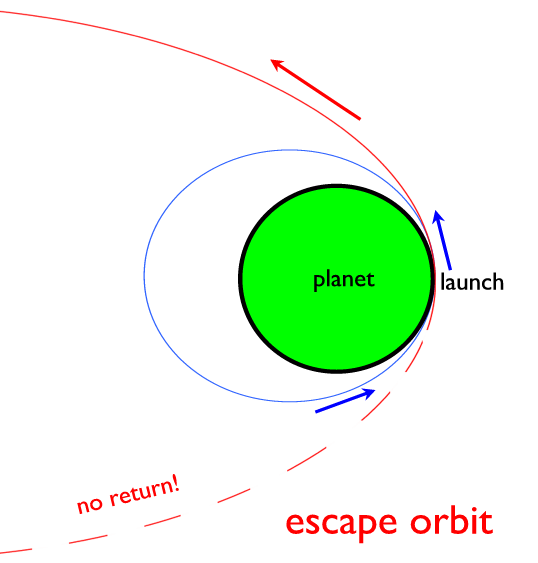
For a large enough launch velocity, the value of a goes to infinity -- the ellipse becomes a parabola, which does not close on itself (red curve in the figure above). If we launch with still larger velocity, the orbit goes from an ellipse to a hyperbola, which doesn't close either. These are escape orbits, so-called because the spacecraft never comes back. The escape velocity is the velocity needed to achieve a parabolic orbit. For the surface of the Earth, the escape velocity is 11.2 km/s. For a planet of mass M and radius r, the escape velocity v is given by the formula
v 2 = 2GM / r
Remember, the escape velocity increases
as the planet's mass M goes up and decreases
as the planet's radius r goes up.